Graph Basics¶
Let \(G = (V, E)\) be a graph. Here is a picture of a graph.
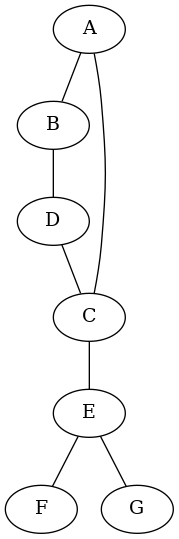
Recall that the elements of V are called vertices, and those of E are called edges. In this example the vertices are \(\{A, B, C, D, E, F, G\}\) and the edges are
Deleting some vertices or edges from a graph leaves a subgraph.
Formally, a subgraph of \(G = (V, E)\) is a graph \(G' = (V', E')\), where \(V'\) is a nonempty subset of V and \(E'\) is a subset of E. Since a subgraph is itself a graph, the endpoints of every edge in \(E'\) must be vertices in \(V'\). For example, \(V' = \{A, B, C, D\}\) and \(E' = \{A—B, B—D, C—D, A—C\}\) forms a subgraph of G.
In the special case where we only remove edges incident to removed nodes, we say that \(G'\) is the subgraph induced on \(V'\) if \(E' = \{( x—y \mid x, y \in V' \text{ and } x—y \in E\}\). In other words, we keep all edges unless they are incident to a node not in \(V'\). For instance, for a new set of vertices \(V' = \{A, B, C, D\}\), the induced subgraph \(G'\) has the set of edges \(E' = \{A—B, B—D, C—D, A—C\}\).
Problem 1¶
An undirected graph G has width w if the vertices can be arranged in a sequence
such that each vertex \(v_i\) is joined by an edge to at most \(w\) preceding vertices. (Vertex \(v_j\) precedes \(v_i\) if \(j < i\).) Use induction to prove that every graph with width at most \(w\) is :math:(w + 1)-colorable.
(Recall that a graph is k-colorable iff every vertex can be assigned one of k colors so that adjacent vertices get different colors.)
Let \(P(n)\) be the proposition defined as a graph, G, of n vertices, for some positive integer n. The graph has a width of w (as defined above), for some \(w \in \Bbb N_+\) where \(0 \le w \le n - 1\)
Theorem: G is (w + 1)-colourable
Base Case: We start with P(1), because for this class we don’t allow empty graphs. \(P(1)\) is true because there is one vertex and zero edges (since we don’t allow loops), which means w is also zero. It follows then, that the graph is \(w + 1\) or 1-colourable. Which is enough colours for the one vertex, so this proves the base case.
Inductive Step: Let G be any (n+1)-node graph. Let w be the width of the graph (as defined above).
If we remove \(v_{n+1}\) we are left with a graph \(G' = (v', e')\). \(G'\) has n vertices, so by P(n) we know it can be coloured with \(w+1\) colours.
The vertex \(v_{n+1}\) is adjacent to at most w other vertices. This means w (or less) of the set of w+1 colours are used to colour its adjacent vertices. Therefore, there exists at least one colour left that can be used to colour \(v_{n+1}\).
So G is (w+1)-colourable. \(\blacksquare\)
Problem 2¶
A planar graph is a graph that can be drawn without any edges crossing.
First, show that any subgraph of a planar graph is planar.
A planar graph, \(G = (V, E)\) has n nodes, and e edges (none of which cross). Removing one node, \(v_n\), gives us a graph \(G' = (V', E')\). Since \(E'\) is a sub-set of E, and none of the edges in E cross, then none of the edges in \(E'\) cross over either. \(\square\)
2. Also, any planar graph has a node of degree at most 5. Now, prove by induction that any planar graph can be colored in at most 6 colors.
Theorem: Let P(n) be the predicate that any n-node planar graph, G, is colourable in 6 or less colours.
Base Case: P(1) is true, because a 1-node graph is actually 1-colourable, which is less than 6 colours.
Inductive Step: We must prove P(n+1) is true, assuming P(n) is true. For P(n+1) we have an (n+1)-node graph, G. Removing a node, \(v_{n+1}\) leaves us with an n-node graph \(G'\) By the inductive hypothesis we know an n-node graph is 6 colourable.
In G, \(v_{n+1}\) is adjacent to at most 5 nodes (by nature of it being a planar graph). This leaves us with at least 1 colour to use on \(v_{n+1}\) for a maximum of 6 colours.
By induction we can conclude any n-node planar graph is at most 6-colourable. \(\blacksquare\)