Equivalence Relations

Problem 1

Intro

Give a description of the equivalence classes associated with each of the following equivalence relations.

a)

Question

Integers x and y are equivalent if \(x \equiv y\ (mod\ 3)\).

\[ \begin{align}\begin{aligned}\lbrack 0 \rbrack = \{ \dots, -9, -6, -3, 0, 3, 6, 9, \dots \}\\\lbrack 1 \rbrack = \{ \dots, -8, -5, -2, 1, 4, 7, 10, \dots \}\\\lbrack 2 \rbrack = \{ \dots, -7, -4, -1, 2, 5, 8, 11, \dots \}\end{aligned}\end{align} \]

b)

Question

Real numbers x and y are equivalent if \(\lceil x \rceil = \lceil y \rceil\), where \(\lceil z \rceil\) denotes the smallest integer greater than or equal to z.

\[[r] = \{ i-1 < r \ge i \}\]

Where r is any real number, and i is the result of \(\lceil r \rceil\) (that is, rounding r up to the nearest whole number).

Problem 2

Intro

Show that neither of the following relations is an equivalence relation by identifying a missing property (reflexivity, symmetry, or transitivity).

a)

Question

The “divides” relation on the positive integers.

Reflexivity holds because any integer can divide itself. Symmetry doesn’t hold because e.g. while \({6 \over 3} = 2\), the reverse is \({3 \over 6} = 0.5\) which is not a positive integer. Transitivity holds because if \(a|b\) and \(b|c\) then a is a common factor of c, e.g. \({6 \over 3} = 2\) and \({12 \over 6} = 2\) so \({12 \over 3} = 4\).

b)

Question

The “implies” relation on propositional formulas.

Reflexivity holds because \(A \Rightarrow A\) gives the same result as itself, e.g. \(T \Rightarrow T = T\) and \(F \Rightarrow F = F\). Symmetry doesn’t hold because while \(A \Rightarrow B\) that does not mean \(B \Rightarrow A\) (if it did then this would be an iff relation). Transitivity holds though, because if \(A \Rightarrow B\) and \(B \Rightarrow C\) then \(A \Rightarrow C\).

Problem 3

Introduction

Here is prerequisite information for some MIT courses:

\[ \begin{align}\begin{aligned}\begin{aligned}\\18.01 & \rightarrow 6.042 \qquad 18.01 && \rightarrow 18.02\\18.01 & \rightarrow 18.03 \qquad 6.046 && \rightarrow 6.840\\8.01 & \rightarrow 8.02 \qquad 6.01 && \rightarrow 6.034\\6.042 & \rightarrow 6.046 \qquad 18.03, 8.02 && \rightarrow 6.02\\6.01, 6.02 & \rightarrow 6.003 \qquad 6.01, 6.02 && \rightarrow 6.004\\6.004 & \rightarrow 6.033 \qquad 6.033 && \rightarrow 6.857\\\end{aligned}\end{aligned}\end{align} \]

a)

Question

Draw a Hasse diagram for the corresponding partially-ordered set. (A Hasse diagram is a way of representing a poset \((A, \preceq)\) as a directed acyclic graph. The vertices are the elements of A, and there is generally an edge \(u \rightarrow v\) if \(u \preceq v\). However, self-loops and edges implied by transitivity are omitted.) You’ll need this diagram for all the subsequent problem parts, so be neat!

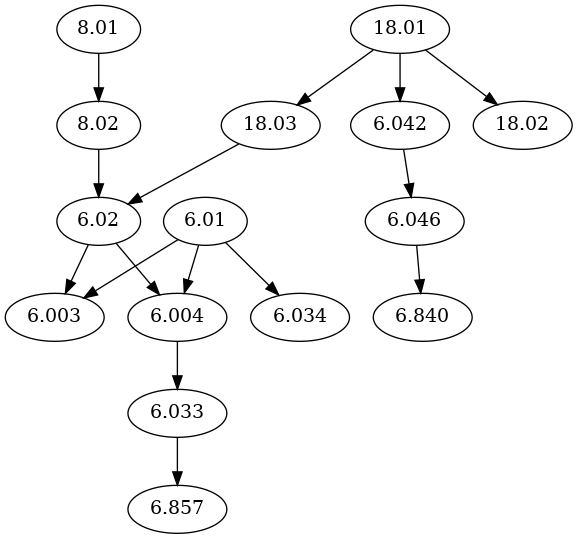
b)

Question

Identify a largest chain. (A chain in a poset \((S, \preceq )\) is a subset \(C \subseteq S\) such that for all \(x, y \in C\), either \(x \preceq y\) or \(y \preceq x\).)

There are two, both of length 6,

\[ \begin{align}\begin{aligned}8.01 \preceq 8.02 \preceq 6.02 \preceq 6.004 \preceq 6.033 \preceq 6.857\\18.01 \preceq 18.03 \preceq 6.02 \preceq 6.004 \preceq 6.033 \preceq 6.857\end{aligned}\end{align} \]

c)

Question

Suppose that you want to take all the courses. What is the minimum number of terms required to graduate, if you can take as many courses as you want per term?

6, because the longest path (aka the critical path) is of length 6.

d)

Question

Identify a largest antichain. (An antichain in a poset \((S, \preceq)\) is a subset \(A \subseteq S\) such that for all \(x, y \in A\) with \(x \neq y\), neither \(x \preceq y\) nor \(y \preceq x\).)

The following graph is ranked by terms vertically. A possible largest antichain is highlighted red,

As you can see this gives an antichain of length 5.

e)

Question

What is the maximum number of classes that you could possibly take at once?

Since the largest antichain is of size 5, this also corresponds to the maximum number of classes you could take simultaneously.

f)

Question

Identify a topological sort of the classes. (A topological sort of a poset \((A, \preceq)\) is a total order of all the elements such that if \(a_i \preceq a_j\) in the partial order, then \(a_i\) precedes \(a_j\) in the total order.)

The following is a topological sort, as calculated by an adaptation of Kahn’s algorithm,

6.01, 6.034, 8.01, 8.02, 18.01, 18.02, 18.03, 6.02, 6.004, 6.033, 6.857, 6.003, 6.042, 6.046, 6.840

g)

Question

Suppose that you want to take all of the courses, but can handle only two per term. How many terms are required to graduate?

8 terms are required as demonstrated by the following graph which has been ranked, so that only 2 courses appear on each level

h)

Question

What if you could take three courses per term?

The minimum number of terms would be 6, as demonstrated below.

Note, this cannot be any lower than 6 because of the critical chain mentioned before.

i)

Question

Stanford’s computer science department offers n courses, limits students to at most k classes per term, and has its own complicated prerequisite structure. Describe two different lower bounds on the number of terms required to complete all the courses. One should be based on your answers to parts (b) and (c) and a second should be based on your answer to part (g).

The longest chain of dependencies will form one lower bound, because no chain can be shorter than the critical path.

The other lower bound is determined by the value of k. According to Dilworth’s lemma, the number of terms is either longer than the longest chain or there is an antichain of size greater than or equal to the total number of courses divided by the length of the longest chain.

Suppose we have length of the longest chain, c, if \({n \over c} > k\) then the number of terms will be greater than c. However if \({n \over c} \le k\) then the number of terms will be at least c.