Travelling Salesperson

3/2-Approximation Algorithm ALG

  1. Construct a graph G whose vertices are the N cities with an edge between every pair of cities \(A \ne B\) with corresponding weight d(A, B), where d(A, B) is the distance between A and B in the plane.

    N = 3

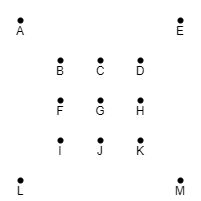
    ../_images/NxN+4.png

  2. Compute an MST T of G (Recall that a minimum spanning tree (MST) of a graph G is a spanning tree whose sum of edge weights is as small as possible).

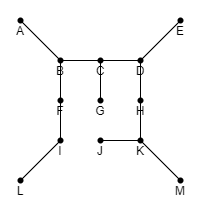
    ../_images/mst.png

  3. Compute, for each city \(A \in G\), the degree \(d_A\) of A in T.

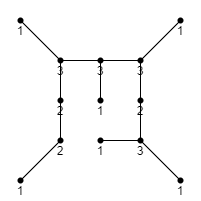
    ../_images/degree-of-mst.png

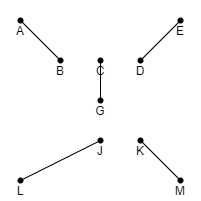
  4. Let \(S = \{A \in G : d_A \text{ is odd}\}\).

    \[S = \{ A, B, C, D, E, G, J, K, L, M \}\]

  5. Compute a minimum weight perfect matching M on the vertices in S (using the distances \(d(\cdot, \cdot)\) as weights).

    ../_images/min-weight-perfect-matching.png

  6. Compute a new set of edges \(E' = M \cup T\). Note that the resulting graph \(G' = (V, E')\) is not necessarily a simple graph since it might contain multiple edges.

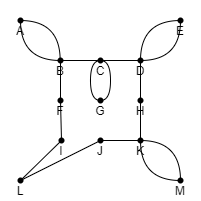
    ../_images/e-prime.png

  7. Take the subgraph \(G' = (V, E')\), and compute an Euler circuit on it.

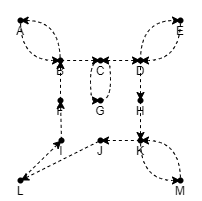
    ../_images/eulers-circuit.png

  8. Use the Euler circuit to give an induced ordering of the vertices (i.e., the order in which the vertices appear for the first time), and do a TSP tour on this order.

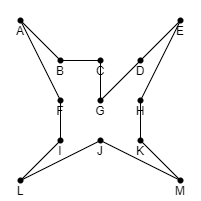
    ../_images/tsp-tour.png

Let OPT be the optimum TSP tour cost.

  1. Show that the cost of any tour is at least the cost of an MST of G. Hence conclude that the cost of an MST is at most OPT.

    An MST, by definition, has a path from any node to any other node. That is, there are edges connecting every node. Also the edges have the minimum weight possible for every node to remain connected. However, OPT requires at least one cycle, because it needs to return to the starting point. If we remove one edge from OPT, we are left with a spanning tree. So we can conclude the sum of the weights in MST is less than the sum of weights in OPT.

  2. Prove that the size of S is even.

    Say we add an edge, e, to a graph connecting 2 nodes, x and y. The degree of x increases by 1, and so does the degree of y. So the sum of degrees on all nodes in the graph increases by 2. Therefore, the sum of degrees must be even.

    We know that the sum of degrees is equal to the sum of odd-degrees and even degrees. Since we just showed the sum of degrees in total is even, then we can conclude that the sum of odd degrees is also even.

    This means we must have an even number of odd degrees.

  3. Prove that the weight of the min weight perfect matching is at most \({OPT \over 2}\).

    The min weight perfect matching (MWPM) has at most \(|V|\) nodes connected by \({|V| \over 2}\) edges. OPT connects every node in the graph, plus 1 to return to the starting point. Suppose the edges in \(wt(OPT) - wt(MWPM) < wt(MWPM)\). But then \(wt(OPT) - wt(MWPM)\) is also a perfect matching, and if it weighs less than the MWPM, that would contradict MWPM being min weight.

    So \(wt(MWPM) \le {wt(OPT \over 2)}\)

  4. Prove that \(G'\) has an Euler circuit, and its cost is at most \({3 \cdot OPT \over 2}\).

    Every node in \(G'\) was either of even degree (and so excluded from S) or odd degree, but then increased by 1 by the perfect matching, making it even. Since every node has even degree, it must have Euler circuit.

    In part 1 we showed \(cost(T) \le cost(OPT)\), and the in part 3 we showed \(cost(M) \le cost({OPT \over 2})\).

    Since \(G'\) is the union of these sets of edges, we get;

    \(cost(OPT) + cost({OPT \over 2}) = cost({3 OPT \over 2})\)

  5. Show that the length of the TSP tour is at most 3OPT/2.

    Since the TSP tour proceeds directly to the next unique node along the Euler circuit it either travels along an edge in the Euler circuit, or it travels directly to it instead of via another node.

    By the triangle inequality we know that a direct edge cannot weigh more than travelling via another node. So \(wt(TSP) \le cost({3 OPT \over 2})\)